辽宁华图_辽宁选调生招聘考试网为您提供辽宁选调生考试备考文章:沈阳选调生考什么科目。更多辽宁选调生招聘信息敬请关注辽宁选调生考试频道(https://ln.huatu.com/xds/)或者关注辽宁华图微信公众号(syhuatu),辽宁华图咨询电话:400-024-1113。华图教育专属客服:点击

60%的定向选调生考试考察行测和申论,如果报考多个省份的选调生一定要注意特殊省份的考试内容!备考有规划~
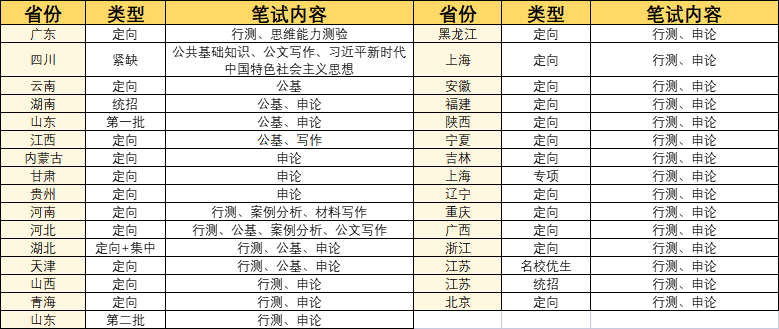
以上这些就是辽宁华图老师为大家分享的辽宁选调生考试文章:沈阳选调生考什么科目,期待大家继续关注同类话题的学习!
辽宁华图小编为您整理辽宁选调生招聘备考技巧
火眼金睛辨“多真多假”
一、如何来识别?
真假推理其实是逻辑判断中的一部分题型,如何来断定这道题是真假推理呢?其实很简单,就是题干中给出若干论断,并且明确真假就是真假推理题。
二、如何解题?
多真多假考察大家的类型题基本上有如下三种:
1.奇数个论断
找多组矛盾关系,矛盾关系的特性是必然存在一真一假,有几组矛盾关系就找几组矛盾关系,矛盾关系外基本只剩一个论断,剩余这个论断真假就能明确。
2.两真两假
先找矛盾关系再找包容关系(推出关系)。
包容关系(推出关系):当题干中一个论断成立能够推出另一个论断也成立,那么这两个论断就构成包容关系。
常考的包容关系:A→A或B;B→A或B;A且B→A;A且B→B等。
当构成推出关系的两个论断是一真一假的时候均为前假后真。
3.假设法
既不存在多组矛盾关系,又无包容关系,就可以采用假设的方法。
如果出现矛盾,则假设不成立;如果没有出现矛盾,则可以直接使用该假设条件。
三、实战演练
【例1】某中药材店开张筹备中,有几个药柜的标签上尚未标注药名,几个进店的消费
者纷纷猜测,甲说:1号柜里是贝母;乙说:2号柜里是三七而且3号柜里不是川芎;丙说:1号柜里肯定不是贝母;丁说:如果2号柜里是三七,那3号柜里就是川芎;戊说:我猜4号柜里是石斛。这时药店老板走进来笑着说:你们中有两个人说错啦。
根据上述叙述。可以推出的是:
A.1号柜里是贝母
B.2号柜里不是三七
C.3号柜里不是川芎
D.4号柜里是石斛
【答案】D
【解析】
第一步,确定题型。
题干有若干论断并且明确真假,确定为真假推理。
第二步,找关系。
甲、丙说的话是矛盾关系,乙、丁说的话是矛盾关系。有两组矛盾关系。
第三步,看其余。
根据矛盾关系的特性“必有一真一假”及题干5个论断2假3真,可知,甲丙中必然有一真一假、乙丁中必然也有一真一假,已经满足两真两假,所以戊一定为真,即4号柜里是石斛。
因此,选择D选项。
【例2】 甲和乙都有可能受邀参加某专家论坛。现在,甲得知了以下消息:
(1)论坛主办方决定,至少邀请甲或乙中的一位;
(2)论坛主办方决定不邀请甲;
(3)论坛主办方一定会邀请甲;
(4)论坛主办方决定邀请乙。
假如上述消息中,两条为真,两条为假,则可推出:
A.论坛主办方决定邀请甲,不邀请乙
B.论坛主办方决定邀请乙,不邀请甲
C.论坛主办方决定同时邀请甲和乙
D.论坛主办方决定既不邀请甲,也不邀请乙
【答案】A
【解析】
第一步,确定题型。
题干有若干论断和真假限定,确定为真假推理。
第二步,找关系。
(2)和(3)为矛盾关系,(1)和(4)为包容关系。
第三步,看其余。
根据矛盾关系的特性“必有一真一假”及题干信息四句论断中两真两假,所以(2)和(3)中必有一真,必有一假,(1)和(4)中也必有一真,必有一假。
(1)和(4)为包容关系,乙→甲或乙,应该“前假后真”,即乙为假,甲或乙为真,那只能甲为真,那么可以推出没有邀请乙,邀请甲。
因此,选择A选项。
【例3】甲、乙、丙、丁四人驾车外出,遇到交警排查酒驾,四人因司机酒后驾车害怕受到惩罚而弃车逃跑,很快被交警擒获。当询问谁是驾驶员时,甲说:“不是我。”乙说:“是甲。”丙说:“不是我。”丁说:“是乙。”
若四人中有且仅有两人说了假话,那么谁一定说了假话?
A.甲
B.乙
C.丙
D.丁
【答案】D
【解析】
第一步,确定题型。
题干有若干论断和真假限定,确定为真假推理。
第二步,找关系。
甲和乙为矛盾关系。
第三步,看其余。
根据矛盾关系的特性“必有一真一假”及题干信息两真两假,不存在多组矛盾关系,又无包容关系,只能采用假设法,可知丙和丁中必有一真,必有一假,即包括两种情况:
(1)丙为假,丁为真,可知:丙和乙均是驾驶员,不能两人同时是驾驶员,出现冲突,排除。
(2)丙为真,丁为假,可知:丙不是驾驶员,乙不是驾驶员,则驾驶员要么是甲,要么是丁,不存在冲突,符合题意。
结合设问方式找“一定”说假话的人,则丁一定说假话。
因此,选择D选项。
分析推理之六面体中的移面大法
基于六面体面与面之间的关系,解决六面体问题的方法主要分为两种:相对面排除法和相邻面排除法。其中,能够适用相对面排除法的题目并不多,所以一般我们解决六面体问题所采用的方法都是相邻面法。但做题过程中我们发现,出题人为了保证六面体题目的难度,题干立体图形当中的相邻面在展开图中并不“相邻“。例如下面这道例题:
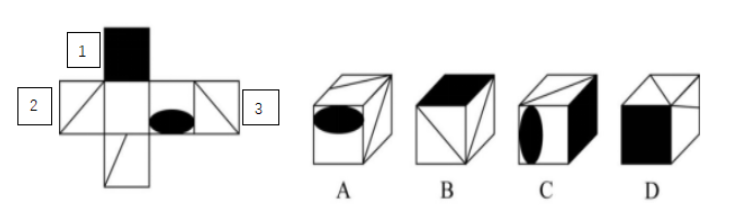
以B选项为例,B项立体图形中展示的相邻面在展开图当中分别标记为1、2、3号,但这三个面在展开图当中并不相邻,因此要想直接验证B项正确与否需要非常强的空间想象能力。
那么有没有一种方法能够将这三个面移动到一起,在展开图当中也呈现相邻的状态呢?这就是要跟大家分享的“移面大法”。
什么是“移面大法”?我们知道,同一个立方体有11种不同的展开方式,我们选择其中一种展开:
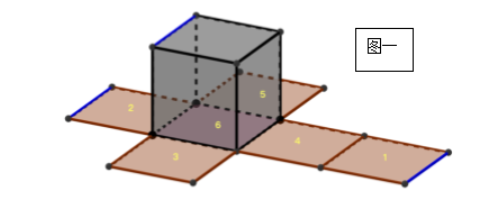
上图是从蓝色楞作为起点,将六面体展开所形成的展开图,展开图中的蓝色边是折成立体图时两个面的公共边。当然,我们也可以再换一种展开方式,比如下图这种从红色楞作为起点的展开方式:
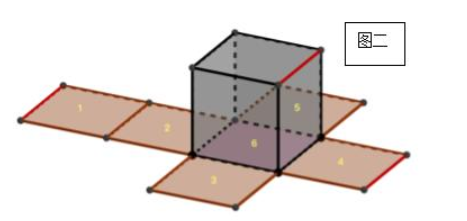
这两个展开图是同一六面体的不同展开方式,对比两图你会发现,1号面在图一中位于4号面的右侧,但在图二中却出现在了2号面的左侧,看上去好像1号面进行“平移”了一样。这就是“移面大法”的第一种移动方式:四面相邻时,最边缘的面可以另一个边缘平移,折成的六面体不变。
再换一种展开方式,如下图:
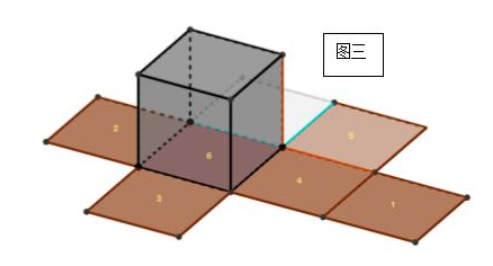
5号面在图一中位于6号面上面,而且两面的公共边在图三中已用蓝色笔标出,而在图三中,5号面出现在了4号面上面,公共边用红色笔标出。这两个展开图也是同一六面体的不同展开方式,对比两图,看上去好像是5号面从图一中原来的位置“旋转”到图三中的位置一样。这就是“移面大法”第二种移动方式:垂直边的两个面将其中一个旋转90°,折成的六面体不变。
以上两种移面方式就是解六面体常用的“移面法”,通过移面,可以进一步使用箭头法、公共边公共点法验证选项。比如,仍以上面的例题为例:
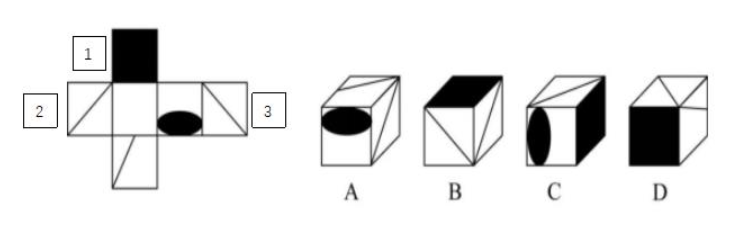
B项中的三个面并不相邻,我们可以通过移面使他们在展开图中变成相邻的面:将1号面进行旋转、2号面进行平移,最终得到的展开图如下图:
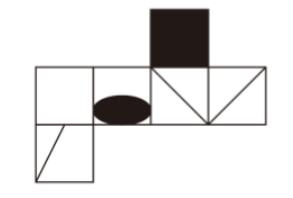
此时,再通过箭头法就能很轻松的判断出B项能由该展开图折叠而成,其他选项留给读者自行验证。
推理分析之快速解决特殊定义叠加题型
一、识别及常规解题方法
定义叠加的出题形式大多都是两段式或九宫格式。图形特征为“图形轮廓和分割区域相同,内部填充不同”。叠加的方法是“相同位置进行运算叠加”。但需要注意的是定义叠加在运算时不遵循数学上的加法交换律,即“黑加白不一定等于白加黑”,需要具体题目具体验证。运算规律也不是每道题统一的,不同的题可能运算规律不一致,需要根据题目给出的已知图形寻找本题的运算规律。
【例】从所给的四个选项中,选择最合适的一个填入问号处,使之呈现一定的规律性:
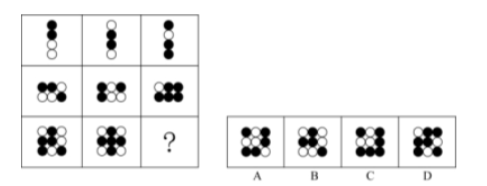
【答案】C
【解析】第一步,观察特征。
元素组成相似,优先考虑样式,并且所有图形外部轮廓都是九宫格,内部颜色有黑有白,优先考虑定义叠加运算。
第二步,九宫格,横向规律较为常见,优先考虑。
第一行,黑+白=黑,黑+黑=白,白+黑=黑,白+白=黑;第二行经验证符合此规律;第三行,应用规律,只有C项符合。
二、识别及快速解题方法
有些定义叠加的题目里面会出现相同颜色的捆绑块,(相同颜色的小块图直接挨在一起)那么相同颜色的捆绑块运算完,该捆绑块的颜色一定也是一致的(是黑全为黑,是白全为白);
这样选项中捆绑块颜色不一致的就可直接排除,可以帮助我们提高解题速度。接下来我们练一下:
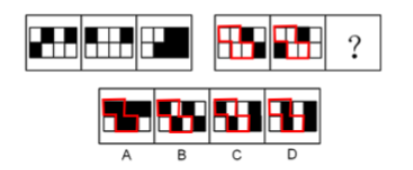
【例1】从所给的四个选项中,选择最合适的一个填入问号处,使之呈现一定的规律性:

【答案】D
【解析】第一步,观察特征。
元素组成相似,优先考虑样式,并且所有图形外部轮廓都是九宫格,内部颜色有黑有白,优先考虑定义叠加运算。
第二步,观察发现,第三行有捆绑块(如图),捆绑块运算完黑白情况应保持一致,只
有D选项符合。
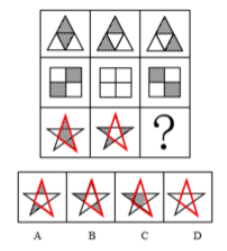
【例2】从所给的四个选项中,选择最合适的一个填入问号处,使之呈现一定的规律性:

【答案】A
【解析】第一步,观察特征。
元素组成相似,优先考虑样式,两段式并且内部颜色有黑有白,优先考虑定义叠加运算。
第二步,观察发现,第二段有捆绑块(如图),捆绑块运算完黑白情况应保持一致,只有A选项符合。
【例3】从所给的四个选项中,选择最合适的一个填入问号处,使之呈现一定的规律性:
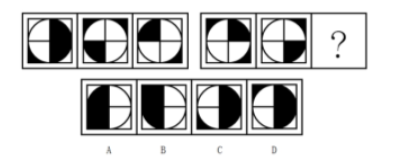
【答案】A
【解析】第一步,观察特征。
元素组成相似,优先考虑样式,两段式并且内部颜色有黑有白,优先考虑定义叠加运算。
第二步,观察发现,第二段有捆绑块(如图),捆绑块运算完黑白情况应保持一致,只有A选项符合。
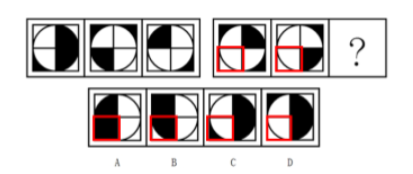
通过这三道题的练习大家会发现,当我们通过观察图形特征,基本锁定考点为定义叠加时,可以看看题干中是否有颜色相同的小块挨在一起,如果有,就可以作为捆绑块,捆绑块的运算结果应保持颜色一致,不一致的可直接排除。希望大家通过本次特殊的定义叠加的学习,能够及时准确地识别出捆绑块,考场上灵活运用,快速解题!











