辽宁华图_国家公务员考试网为您提供2025国家公务员考试文章:2025年阜新市国家公务员考试公务员公告_国考历年进面分数线汇总。更多2025年国家公务员招聘信息敬请关注辽宁国家公务员考试频道(http://ln.huatu.com/guojia/)或者关注辽宁华图微信公众号(syhuatu),辽宁华图咨询电话:400-024-1113。国家公务员考试专属客服:点击
辽宁华图小编为您整理国家公务员考试文章:2025年阜新市国家公务员考试公务员公告_国考历年进面分数线汇总
2025年国家公务员考试公告已于2024年10月14日在国家公务员局发布,2024年10月15日15:30至10月24日115:30开始报名,11月30、12月1日笔试。为了考生能够及时查看国家公务员考试详细,辽宁华图教育小编为大家整理如下:
| 2025辽宁国家公务员考试网 | |||
| 公告 | 国考简章 | 国考职位表 | 国考报名时间 |
| 资讯 | 国考考试时间 | 国考报考指导 | 国考考试内容 |
| 资料 | 国考行测试题 | 国考申论试题 | 国考历年分数线 |
| 备考 | 笔试课程 | 网络课程 | 图书教材 |
点击查看:2025年国家公务员考试公告>>>>
点击查看:2025国家公务员考试职位表>>>>
点击查看:2025年国家公务员考试大纲>>>>
点击查看:2025年国家公务员考试笔试课程>>>>
点击查看:2025年国家公务员考试热门图书>>>>
>>>>>>扫码随时咨询考试相关问题,领取资料试题


因篇幅有限,仅展示部分地市,完整版可扫码免费获取!
以上这些就是辽宁华图老师为大家分享的2025国家公务员考试文章:2025年阜新市国家公务员考试公务员公告_国考历年进面分数线汇总,期待大家继续关注同类话题的学习!
相关信息推荐:
辽宁华图小编为您整理国考备考技巧
三招搞定真假话
例1
现有甲、乙、丙三人同时说了以下三句话
甲说:“乙正在说谎”
乙说:“我没有说谎”
丙说:“他俩正在说谎”根据三人的对话情况,有几人说假话
A.1
B.2
C.3
D.0
【华图解析】正确答案为B,首先确定是否是真假话问题,判断依据出现真假语句,其次就是有没有直接的矛盾关系,然后利用矛盾判断关系判断其他条件,最后选择正确答案,题干中问题明显有真假语句,分析题干可以找到甲乙条件为矛盾关系,矛盾的性质必有一真一假,再由此判断丙的话语是否正确,题干丙说甲乙均为假此话必然错误,结合甲乙矛盾必有一真一假,可以得出有两人为假话。因此正确答案为B。
结合上述题干我们可以总结遇到真假话问题,大家不要紧张,依托三步骤既可以解决问题,第一步寻找矛盾关系,第二步跳出矛盾关系判断其他条件的真假,一般情况就可以寻找正确答案了,当然如果此时还是无法解决问题,利用第三步将判断的条件带回矛盾确定互为矛盾的条件中谁真谁假,此时大多数问题就可以轻松解决。针对真假话问题,考的最多的题型,就是一真一假以及两真两假,例题1就是常见的一真一假问题,接下来我们看一下两真两假问题又该如何用三步解决呢?
例2
学校在为失学儿童募捐活动中收到两笔没有署真名的捐款,经过多方查证,可以断定是周、吴、郑、王中的某两个捐的。经询问:
周说:“不是我捐的”
吴说:“是王捐的”
郑说:“是吴捐的”
王说:“我肯定没有捐”
最后经过详细调查证实四个人中有两个人说的是真话
根据已知条件,请你判断下列哪项可能为真?()
A.是吴和王捐的
B.是周和王捐的
C.是郑和王捐的
D.是郑和吴捐的
【华图解析】正确答案为C,首先判断题型问法出现真假话语表述,确定为真假问题,接着分析题干条件是否存在矛盾关系,发现“吴”“王”互为矛盾必有一真一假,但题干信息是两真两假,此时另外两个条件也是必有一真一假,但不是矛盾关系,我们可以对另外两个条件进行假设,假设其中一个为真,则另外一个为假,进行验证,假设周为真,则郑为假,得到信息为“非周、非吴”,结合题干四人中由两人参与排除周和吴即郑和王参与,得出选项为C。
隔年增长率的计算
在行测资料分析的高频考点中,增长一直占据重要位置。其实,除了我们常见的普通增长,还有一些特殊的增长也会考察。而今天我们就一起讨论下一个特殊的增长——隔年增长。当然,除了隔年增长的基本公式,华图教育带大家一起来看下隔年增长如何拓展应用。
一、隔年增长率的概念
什么是隔年增长率呢?例如:假设2022年的同比增长率为q1,2021年的同比增长率为q2,则2022年比2020 的增长率,我们称之为隔年增长率。
二、基本公式
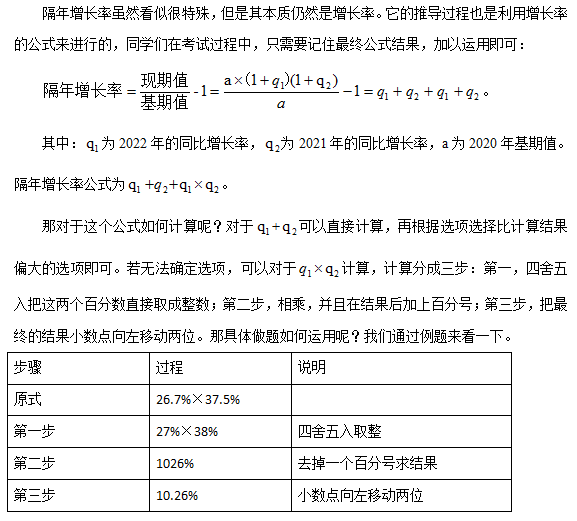
三、典型例题
例1
2021 年,全国共投入研究与试验发展(R&D)经费 27956.3 亿元,比上年增加 3563.2 亿元,增长 14.6%,上年增速为 10.2%;研究与试验发展(R&D)经费投入强度 (与国内生产总值之比)为 2.44%,比上年提高 0.03 个百分点。按研究与试验发展(R&D) 人员全时工作量计算的人均经费为 48.9 万元,比上年增加 2.3 万元。
问题:与 2019 年相比,2021 年全国研究与试验发展(R&D)经费约增长了:
A.14.6%
B.10.2%
C.26.3%
D.24.8%
【华图解析】 C。由材料可知,2021 年,全国共投入研究与试验发展(R&D) 经费比上年增长 14.6%,上年增速为 10.2%。所求为 14.6%+10.2%+14.6%×10.2%>14.6% +10.2%=24.8%,符合题意的只有 C 项,选择 C。
例2
2020年我国生鲜零售市场规模超 50395 亿元,同比增长 4.9%。生鲜电商行业市 场规模达 4658.1 亿元,同比增长 27.9%,上年为增长 42.5%。我国生鲜电商渗透率为 7.91%,较上年增长 1.93%。
问题∶ 与2018年相比,2020年我国生鲜电商行业市场规模约上升了∶
A.26.5%
B.58.5%
C.71.6%
D.82.3%
【华图解析】D。根据题干,2020年我国生鲜电商行业市场规模同比增长27.9%,上年为增长42.5%,则根据隔年增长率公式,列式为 27.9%+42.5%+27.9%×42.5%≈70.4%+28%×43%≈83%,对应的选择D选项。
最值代入秒杀技巧
代入法是公务员考试中经常会用到的一种快速计算方法,经常用于类似以下描述的题目中:“一个数”满足某种特点,或题目中所要求解的数据在选项中都已经给出。特别地,如果题目问“最大、最多”等,一般先从值最大的选项开始代入,如果值最大的选项不符合,再代入值“第二大的”选项。如果题目问“最小、最少”等,一般先从值最小的选项开始代入,如何值最小的选项不符合,再代入值“第二小的”选项,这就是最值代入的思维方法。
【例1】(2019年北京)某工厂有甲、乙、丙3条生产线,每小时均生产整数件产品。其中甲生产线的效率是乙生产线的3倍,且每小时比丙生产线多生产9件产品。已知3条生产线每小时生产的产品之和不到100件且为质数,则乙生产线每小时最多可能生产多少件产品?( )
A. 14
B. 12
C. 11
D. 8
【答案】A
【解析】设乙生产线每小时生产x件产品,则甲生产线每小时生产3x件产品,丙生产线每小时生产3x-9件产品,3条生产线每小时生产的产品之和为7x-9件。问乙生产线每小时最多可能生产多少件产品,可从值最大的A选项开始代入,如果x=14,则7x-9=89是质数,符合题意。
因此,选择A选项。
【例2】(2020年北京)某单位有不到 100 人参加远足活动, 如将该单位人员平均分成 N 组 (N>1 且 每组人数>1), 则每组的人数有且仅有6 种不同的可能性。 则该单位参加活动的人数可能的最小值和最大值之间相差多少人? ()
A. 32
B. 48
C. 56
D. 64
【答案】D
【解析】本题考查约数倍数问题。该单位的人员总数能平均分成N组,要求其中N>1且每组人数>1,设每组人数为M,则总人数=N×M。由题意M有且仅有6种不同可能,即总人数应该有且仅有除了1和本身之外的6个约数。100以内除了1和本身外有6个约数的至少是2×2×2×3=24(约数为2、3、4、6、8、12),代入选项,从最大的D开始,相差64则最大是88,约数除了1和88外有2、4、8、11、22、44共6个,满足题意。
因此,选择D选项。
【例3】(2019年1201广东选调)某单位组织趣味运动会,运动会一共安排了8个项目。一个项目结束之后才开始下一个项目。如果每个项目每支队伍都要派出4人参加,同时每个队员参赛项目不超过3个。则每支队伍至少需要( )名队员。
A.11
B.12
C.13
D.14
【答案】A
【解析】数量关系-数学运算-最值问题。每支队伍的参赛人次数是8×4=32(人次),由于每人最多参加3次,求每支队伍队员人数的最小值,可以利用选项最小值代入法,代入A项,最小的11人可参赛33次,符合要求。
因此,选择A选项。











