辽宁华图_辽宁公务员考试为您提供2025辽宁省公务员考试备考文章:丹东省考报名时间是几月。更多2025年辽宁公务员招聘信息敬请关注辽宁公务员考试频道(http://ln.huatu.com/gwy/)或者关注辽宁华图微信公众号(syhuatu),辽宁华图咨询电 话:400-024-1113。辽宁公务员考试专属客服:点击
辽宁华图小编为您整理辽宁公务员考试备考文章:丹东省考报名时间是几月
( 点击图片查看报名入口:2025年1月19日9:00至1月23日24:00)
2025年辽宁公务员考试公告已于2025年1月 16日在辽宁人事考试网发布,此 次全省招录6511个岗位共计7841人!网上报名时间:2025年1月19日9:00至1月23日24:00。已缴费的报考者,打印准考证时间2025年3月10日9:00至3月16日9:00,登录辽宁人事考试网,自行打印准考证、报名登记表(A4纸,一式两份),并妥善保管。笔试时间:2025年3月15日,9:00至11:00《行政职业能力测验》;14:00至16:30《申论》。2025年3月16日,9:00至11:00《专业科目》。
点击查看:2025年辽宁公务员考试公告>>>>
点击查看:2025年辽宁公务员考试职位表>>>>
>>>>>>扫码随时咨询公务员考试相关问题,领取资料试题

以上这些就是辽宁华图老师为大家分享的2025年辽宁公务员考试文章:丹东省考报名时间是几月,期待大家继续关注同类话题的学习!
相关信息推荐:
辽宁华图小编为您整理辽宁省考备考技巧
数字特性法巧解数量关系
解决数量关系常用的方法有几下几种:
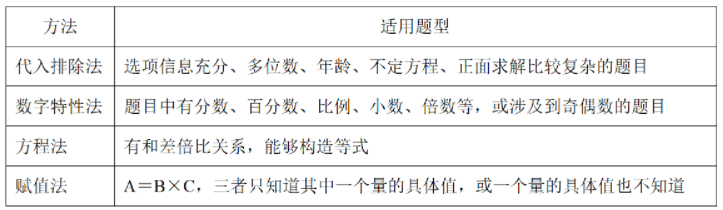
对于以上4种方法,数量大多数题目都可以用代入排除法来做,只不过适用题型的题目用代入排除法求解会更简单;方程法是大家从小学就接触的一种方法,常见的就是一元一次方程和二元一次方程;赋值法大家也不陌生,它可以广泛应用于工程、行程、经济利润等问题;数字特性法是我们快速解决数量关系的一种方法,关于数字特性的主要知识点详见下面的思维导图:
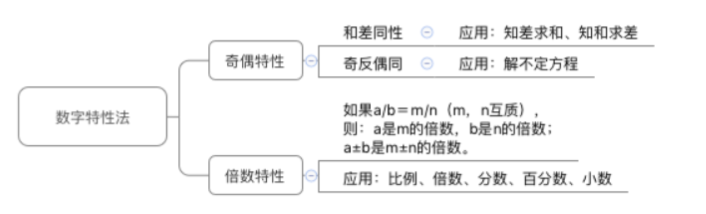
接下来我们就来看几道真题,详细阐述一下怎么利用数字特性来巧解数量关系题目。
【例1】某旅游公司有能载4名乘客的轿车和能载7名乘客的面包车若干辆,某日该公司将所有车辆分成车辆数相等的两个车队运送两支旅行团。已知两支旅行团共有79人,且每支车队都满载,问该公司轿车数量比面包车多多少辆?
A.5
B.6
C.7
D.8
【图图点拨】题目问轿车数量比面包车多多少辆,即考查轿车数量与面包车数量的差值,根据奇偶特性的和差同性原则,轿车数量与面包车数量的和是偶数(题目说将所有车辆分成车辆数相等的两个车队运送两支旅行团),所以轿车数量与面包车数量的差也是偶数,排除A、C。接下来小伙伴不继续往下做,也有1/2的概率蒙对。继续往下做只要从B、D选项中随便代入一个到题干中就可以了,比如代入B选项,设轿车有x辆,面包车有y辆,那
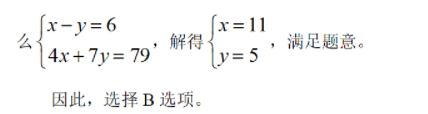
例1是关于数字特性法中奇偶特性的应用,下面我们再来看一道题目。
【例2】A和B两家企业2023年共申请专利300多项,其中A企业申请的专利中27%是发明专利,B企业申请的专利中,发明专利和非发明专利之比为8︰13。已知B企业申请的专利数量少于A企业,但申请的发明专利数量多于A企业,问两家企业最少申请非发明专利多少项?
A.237
B.242
C.250
D.255


数量关系万变不离其宗的题型:和定最值
在行测考试当中,数量关系因其自身多变,使很多同学头痛不已,但是有一类型题目只要掌握的了解题方法的本质,不论题目的形式如何七十二变,我们都可以从容应对。在这类型题目中,最典型的就是和定最值问题。接下来华图教育带大家一起来了解:什么是和定最值,以及在考试中如何让和定最值逃不出各位考生的“五指山”。
题型特征
已知几个数的和是定值,求其中某个量的最大值或者最小值。
解题原则
在和为定值的情况下,求其中某个量的最大值,则让其他量尽可能小;求其中某个量的最小值,则让其他量尽可能大。
例1
五人参加百分制考试,成绩总和为328分,已知五人都及格了,成绩均为整数且互不相等,则五个人中成绩最好的最多得了多少分?
A.80 B.81 C.82 D.83
【华图解析】C。题干中描述五人成绩总和为定值,求成绩最好的最多得了多少分,即求其中某个量的最大值。符合和定最值的题型特征。所以求这五人中第一名得分的最大值,就是让其他四人的得分尽可能地小。对于得分最少的是第五名,同时要满足成绩及格且为正整数,所以第五名最少得分为60分。紧接着,第四名的得分要高于第五名,且为正整数,所以第四名最少得分为61分。同理,第三名和第二名的得分分别为62分和63分。根据五人成绩总和为328分,第一名的得分=328-(63+62+61+60)=82分,故本题选C。
例2
某连锁企业在10个城市共有100家专卖店,每个城市的专卖店数量都不同。如果专卖店数量排名第5多的城市有12家专卖店,那么专卖店数量排名最后的城市,最多有几家专卖店?
A.2 B.3 C.4 D.5
【华图解析】C。由题意可知,10个城市专卖店的总数一定,求排名最后的城市最多有几家专卖店,即求其中某个量的最大值。符合和定最值的题型特征。所以求排名第10的城市所拥有的专卖店的数量的最大值,只要让其他9个城市所拥有的专卖店数量尽可能的少即可。而在这9所城市中,最少的是第9名,当第9名最接近第10名时第9名最少,那我们不妨把第10名用x来表示,则第9名为x+1。同理,第8名,第7名和第6名的专卖店数量分别为x+2,x+3,x+4。已知第5名的城市有12家专卖店,由于第4名、第3名、第2名、第1名应尽可能少,但又要比第5名多,因此分别为13、14、15、16家。最后,利用专卖店总和为100家,可得16+15+14+13+12+(x+4)+(x+3)+(x+2)+(x+1)+x=100,则x=4,故本题选C。
例3
一次数学考试满分为100分,某班前六名同学的平均分为95分,排名第六的同学得86分,假如每个人得分是互不相同的整数,那么排名第三的同学最少得多少分?
A.94 B.97 C.95 D.96
【华图解析】D。题干已知前六名的平均分,相当于知道了前六名成绩之和为定值,求第三名最少得多少分?符合和定最值的题型特征。要求第三名最少多少分,也就是让其他五人的得分尽可能地多。最多的是第一名,得分为100分。而第二名的得分尽可能多且每个人的得分为互不相同的整数,所以第二名得分为99分。紧接着,当第四名的得分最接近第三名时,第四名得分最多,那我们不妨先把第三名用x来表示,所以第4名为x-1。同理,第5名得分为x-2。那么根据六个人成绩之和为95×6=475,可以得到100+99+x+(x-1)+(x-2)+86=475,则x=96,故本题选D。
行测经济利润问题巧解法
赋值法指的是给予题干当中的未知数一个特殊的特定值,以便达到快速解题的效果。适用于题干中出现大量的比例、百分数或分数时,或者题干的变量满足A=B×C的关系,且未给出明确数值时。
经济利润问题常用解题公式满足A=B×C的关系,例如:总利润=单件利润×销量,总销售额=单件售价×销量。大体有以下两种赋值情况:
一、题干中出现百分数、分数、比例,并给出其中两项B和C,这时当A不变时,可以给A进行赋值,赋值为B和C的最小公倍数。当A变化时,给B或C进行赋值。
例1.某矿业产品公司支付了一批货款,一半用于购进每吨400元的A型石英矿,另一半用于购进每吨600元的B型石英矿,则A、B两种石英矿的平均价格是每吨多少元?
A.480B.490
C.500D.510

例2.某楼盘的地下停车位,第一次开盘时平均价格为15万元/个;第二次开盘时,车位的销售量增加了一倍、销售额增加了60%。那么,第二次开盘的车位平均价格为多少?
A.10万元/个B.11万元/个
C.12万元/个D.13万元/个
【答案】C。解析:本题求平均价格,在本题中销售额=平均价格×销售量。从“第二次开盘销售额增加了60%”可知销售额是存在变化的,因此可以给销售量进行赋值。给第一次开盘的销售量赋值为10个,则第一次开盘的销售额为150万。第二次销售量增加了一倍变为20个,销售额增加了60%变为240万,因此第二次的平均价格为12万元/个,本题选择C。
例1和例2的题干都满足A=B×C的关系,并且给出了其中一个变量的具体数值。例1中,A不变,因此给A进行赋值;例2中,A存在变化,因此给B或C进行赋值。
题干中出现百分数
、分数、比例,但任何具体数值都未给出,可以进行双赋值。
例3.某企业引进新技术后,原材料成本降低了40%,单位人工成本上涨了80%,所需要的工人数降低为原来的一半。已知采用新技术前,总人工成本为原材料成本的4倍,则采用新技术后总人工成本是原材料成本的多少倍?
A.1 B.2 C.3 D.4
E.5 F.6 G.7 H.8
【答案】F。解析:本题题干中总人工成本=单位人工成本×工人数,并未给出任何一个量的具体数值,因此,可以进行双赋值。在引用新技术之前,赋单位人工成本为100元/人,工人数也为100人,则总人工成本为10000元,原材料成本为2500元;引进新技术之后,单位人工成本上涨了80%,即变为180元/人,工人数降低为原来的一半,即变为50人,则总人工成本为9000元,原材料成本降低了40%,即变为1500元。9000÷1500=6,因此,采用新技术之后总人工成本是原材料的6倍,本题选择F。
例3中,题干满足A=B×C的关系,但是没有给出了任何一个变量的具体数值。因此,可以给B和C进行双赋值。











