沈北华图_辽宁公务员考试网为您提供2022辽宁省公务员考试备考文章:已发布!2022年辽宁省考招录职位表。更多2022年辽宁公务员招聘信息敬请关注辽宁公务员考试频道(http://ln.huatu.com/gwy/)或者关注辽宁华图微信公众号(syhuatu)。
沈北华图小编为您整理辽宁公务员考试备考文章:已发布!2022年辽宁省考招录职位表

( 长按识别二维码获取全部职位表)
长按识别二维码获取全部职位表)
2022年辽宁省公务员考试共招录5269人,4295岗!辽宁华图小编为您整理出各地市及法院、检察院以及监狱系统招录人数及岗位数。具体详情详见下表:
| 2022年辽宁省考各地市职位表 | |||
| 地市 | 招录人数 | 岗位数 | 职位表下载 |
| 鞍山 | 181 | 174 | 2022辽宁省考鞍山地区职位表 |
| 本溪 | 210 | 175 | 2022辽宁省考本溪地区职位表 |
| 朝阳 | 334 | 279 | 2022辽宁省考朝阳地区职位表 |
| 大连 | 417 | 402 | 2022辽宁省考大连地区职位表 |
| 丹东 | 259 | 251 | 2022辽宁省考丹东地区职位表 |
| 法院 | 778 | 491 | 2022辽宁省考法院系统职位表 |
| 抚顺 | 220 | 201 | 2022辽宁省考抚顺地区职位表 |
| 阜新 | 114 | 114 | 2022辽宁省考阜新地区职位表 |
| 葫芦岛 | 265 | 254 | 2022辽宁省考葫芦岛地区职位表 |
| 监狱 | 663 | 264 | 2022辽宁省考监狱戒毒系统职位表 |
| 检察院 | 246 | 215 | 2022辽宁省考检察院系统职位表 |
| 锦州 | 402 | 374 | 2022辽宁省考锦州地区职位表 |
| 辽阳 | 170 | 157 | 2022辽宁省考辽阳地区职位表 |
| 盘锦 | 172 | 165 | 2022辽宁省考盘锦地区职位表 |
| 沈抚 | 10 | 9 | 2022辽宁省考沈抚新区地区表 |
| 沈阳 | 300 | 295 | 2022辽宁省考沈阳地区职位表 |
| 铁岭 | 276 | 246 | 2022辽宁省考铁岭地区职位表 |
| 营口 | 134 | 130 | 2022辽宁省考营口地区职位表 |
| 省直 | 118 | 99 | 2022年辽宁省考省直系统职位表 |
辽宁华图小编对2022年辽宁省考职位表做了简单的分析:其中三不限岗位招录25人共计23个岗位,以乡镇、街道岗位为主!应届毕业招录岗位占总岗位的57.64%。

图书推荐:
2022辽宁公务员6本套+2022版公务员考试必刷10000题
沈北华图小编为您整理辽宁省考备考技巧用最小公倍数巧解植树问题
在行测数量关系模块中,植树问题一直以来都是公务员考试中考查频率比较高的知识点。从基础的植树问题再到植树问题与最小公倍数或最大公约数关联,都有涉及到。针对这类题目,只要能够掌握基本的理论知识与内在联系,勤加练习,相信在考场上就可以轻松应对,拿到分数。今天我将在这里针对植树问题与最小公倍数综合考查类题目进行详细讲述,梳理它们之间的关系,帮助大家建立起系统的知识框架,掌握其中的技巧。
题目类型
植树问题,顾名思义,即涉及到植树类的题目,包含直线单侧植树、两侧植树、楼间植树与环形植树。当然,不仅仅是单一的植树,安装路灯、摄像头、挖洞插旗杆等间隔一定距离工作的类型都属于植树问题,需要用植树的思维去解答。
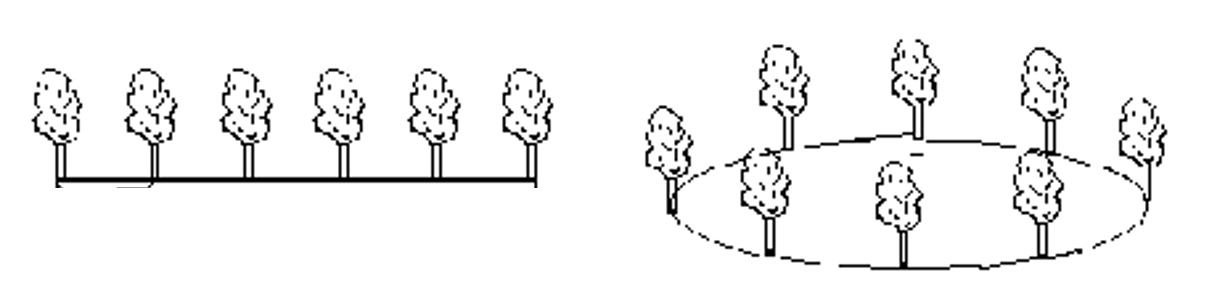
解题思路
首先掌握基础知识:

再考查植树与最小公倍数的关系:
例如,一段固定长度的街道,原来每隔5米种一棵树,说明每棵树所在的位置为5的整数倍,后面改为4米一棵树,说明之后每棵树所在的位置为4的整数倍,那么如果有某些位置既是5的整数倍,又是4的整数倍,即5和4的公倍数,这些位置的树就不需要挪动,这些位置和5、4的最小公倍数相关,整段路有多少个这样的公倍数,就有几个位置已经在第一次的间隔中被种植或者安装,调整间隔种植时,不需要调整或移动,即不需要挪动的位置数=路长/前后距离的最小公倍数(注意计算直线路段不需要挪动树的棵数时依然要考虑加1或减1)。
思路运用
【例1】施工队给一个周长为40米的圆形花坛安装护栏,刚开始,每隔1米挖一个洞用于建栏杆。后来发现间隔太远,决定改为每0.8米挖一个洞。那么至少需要再挖( )个洞。
A.39
B.40
C.41
D.42
【答案】B
【解析】第一步,可知题目中涉及间隔一定距离工作,为植树问题;
第二步,环形挖洞的个数=40/0.8=50个洞,但由于之前已经存在了一些洞,若是洞重合,则无需再挖,之前每个洞所在的位置为1米的整数倍,之后每个洞所在的位置为0.8米的整数倍,则它们最小公倍数的位置是重合的,不需要再重新挖,共有40/10=10个洞重合(4为0.8米与1米的最小公倍数)。至少还需再挖50-10=40个洞。
因此,选择B选项。
【例2】某公园举办春节花展,在周长400米的中心区布置了环形花槽,并在花槽上每隔16米挂一只灯笼,不久后元宵灯会临近,公园决定增加并挪动一些灯笼,但仍保持灯笼间距相等。已知加入新灯笼后,共有5只旧灯笼没有移动,则调整后的灯笼间距最大为( )米。
A.12
B.10
C.8
D.5
【答案】B
【解析】第一步,根据题目意思,5只没有移动的灯笼把花槽分成5段,每段长为400÷5=80(米);
第二步,设增加一些灯笼后间距为x米,原间距是16米,没有移动的灯笼间距为两次加入灯笼间距的最小公倍数,则16与x的最小公倍数为80。代入选项,只有B、D选项两个数字与16的最小公倍数为80。题目要求间隔最大,则增加灯笼后的间距为10米。
因此,选择B选项。
通过上述两个植树问题与最小公倍数综合考查的题目不难发现,在植树问题中,涉及到前后两次间隔距离调整,那么两个距离公倍数的位置不需要再重新操作。不管是正面还是反面考查,只有将其原理掌握,才能一举拿下。
思路总结
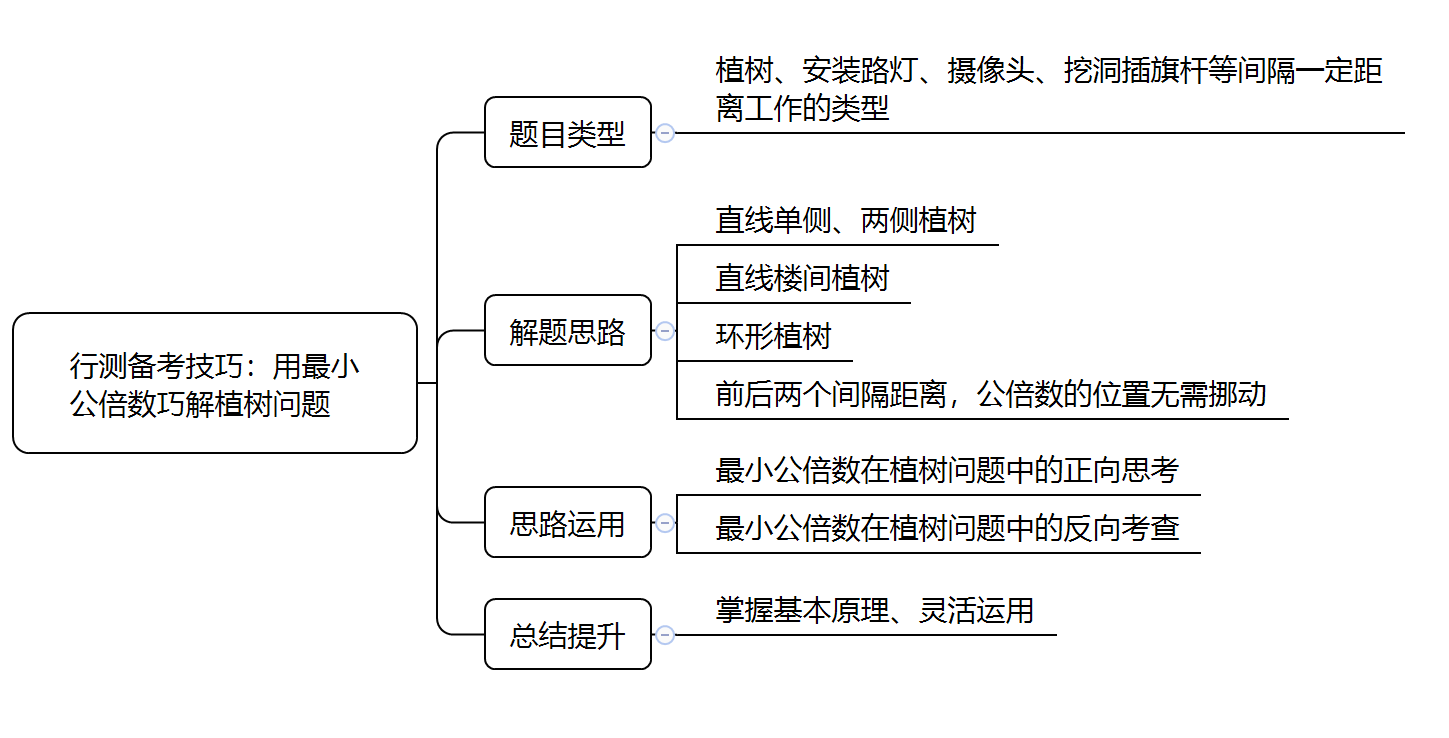
数量关系中神奇的“赋值法”
数学运算中经常会遇到一种题目,它的题干没有给出具体数据的时候,题目问的也是相对情况,对于这样题,很多考生都会纳闷,题干都没有给,我们怎么求?其实,遇到这类题,考生不必感到慌张,因为,此类题目可以通过“赋值法”来快速破题。接下来本文将详细介绍此类题目的解题方法“赋值法”。
1.“赋值法”的定义
赋值法是一种解题思想,那么它是一种什么样的思想呢?所谓的“赋值法”就是人为地给某个未知量赋为具体数据。那么,我们就有必要明确何为具体数据,具体数据是指带单位的数据,如50万元就是具体数据,又比如1/3,它没有单位,所以不能称之为具体数据。
2.“赋值法”的适用场景
赋值法虽然可以人为地给某个未知量赋为具体数据,但是赋值法也不是随时随地随心所欲地使用,要采用赋值法就必须要满足题干“缺量”这么一个条件,而“缺量”具体体现在以下两种情形。
①题干形成了A=B×C等这样的三量关系,而且这三个量最多给出一个量的具体数据。如工程问题中,存在“总量=效率×时间”这样的三量关系,如果题目只给出时间,效率和总量并没有给出,则满足“形成了A=B×C的三量关系,而且这三个量最多给出一个量的具体数据”,则可用赋值法。
②题干一个具体数据都没有,题干给出来全都是分数、百分数、倍数、比例这些信息。
需要注意的是,以上两种情形,只要满足其一,就可以判定该题可以采用赋值法。
3.“赋值法”的赋值原则
在确定可以采用赋值法之后,接下我们就要思考怎么赋值才能更有利于解题。赋值的目的是为了帮助我们解题,那么解题时我们也希望计算简单,因此,在赋值时我们要遵循一个根本原则——好计算,人为赋予的数据应该让该题的计算简单、容易。一般来说好计算可以体现在在4个原则:
原则一:赋最小公倍数
原则二:赋比例份数
原则三:赋乘法
原则四:赋不变的量
这4个赋值原则,我们需要注意3点,一是这4个原则不是互相排斥互相独立,它们是相辅相成,甚至可以混合使用的;二是赋值原则包含但不限于这4个原则;三是赋值的根本原则是好计算,所以在赋值时应该具体问题具体分析,而不是刻板的使用所谓的赋值原则。
4.例题讲解
【例1】某楼盘的地下停车位,第一次开盘时平均价格为15万元/个;第二次开盘时,车位的销售量增加了一倍、销售额增加了60%。那么,第二次开盘的车位平均价格为:
A.10万元/个B.11万元/个
C.12万元/个D.13万元/个
【答案】C
【解析】根据题干形成“销售额=平均价格×销售量”的三量关系,这三量关系中只有平均价格是具体数据,因此可用赋值法解题。因为题目给出第一次开盘的平均价格为15万元/个,因此赋第一次开盘的销售量为1个,则第一次开盘的销售额为15×1=15万元。根据题干信息“第二次开盘时,车位的销售量增加了一倍、销售额增加了60%”,可求第二次开盘的销售量=1×2=2个,销售额=15×(1+60%)=24万元,则根据公式平均价格=销售额÷销售量=24÷2=12万元/个。因此选择C选项。
【例2】高架桥12:00~14:00每分钟车流量比9:00~11:00少20%,9:00~11:00、12:00~14:00、17:00~19:00三个时间段的平均每分钟车流量比9:00~11:00多10%。问17:00~19:00每分钟的车流量比9:00~11:00多:
A.20%B.30%
C.40%D.50%
【答案】D
【解析】已知题干给出的信息全是百分数,一个具体数据都没有,因此可用赋值法解题。赋值9:00—11:00每分钟车流量为10,则12:00—14:00每分钟车流量为10×(1-20%)=8,三个时段每分钟车流量的平均值为10×(1+10%)=11。则17:00—19:00每分钟车流量为11×3-10-8=15。故17:00—19:00每分钟车流量比9:00—11:00多50%。因此,选择D选项。
通过上面的例子,我们发现遇到一些“缺量”的题目时可以采用赋值法,赋值法也确实可以帮助考生快速破题。当然,赋值法也不是一成不变的,各位考生应该灵活应用,想要了解更多的赋值法内涵,各位考生可继续关注华图教育。