辽宁华图_国家公务员考试网为您提供2024国家公务员考试文章:2024年沈阳国考公务员公告。更多2024年国家公务员招聘信息敬请关注辽宁国家公务员考试频道(http://ln.huatu.com/guojia/)或者关注辽宁华图微信公众号(syhuatu)。国家公务员考试专属客服:点击
辽宁华图小编为您整理国家公务员考试文章:2024年沈阳国考公务员公告
点击查看:2024年国家公务员考试公告>>>>
2024年国家公务员考试公告已于2023年10月14日在国家公务员局发布,考生可于2023年10月15日8:00至10月24日18:00期间登录“中央机关及其直属机构2024年度考试录用公务员专题网站”(http://bm.scs.gov.cn/kl2024)进行网上报名,公共科目笔试将于11月25、26日在全国各直辖市、省会城市、自治区首府和部分较大的城市同时举行。
点击查看:2024国家公务员考试职位表>>>>
点击查看:2024年国家公务员考试大纲>>>>
>>>>>>扫码随时咨询考试相关问题,领取资料试题

图书推荐:
以上这些就是辽宁华图老师为大家分享的2024国家公务员考试文章:2024年沈阳国考公务员公告,期待大家继续关注同类话题的学习!
相关信息推荐:
辽宁华图小编为您整理国考备考技巧
判断推理技巧:翻译推理之逆否定理介绍
接触过判断推理的同学都知道,判断的众多题型中,最“烧脑”的莫过于逻辑判断,而逻辑判断也分为很多类别,比如翻译推理、分析推理、真假推理。想要学好逻辑判断,首先想要打好基础,就得学好翻译推理。为什么说翻译推理是学习其他逻辑推理的基础呢?刷过大量题目的同学会发现,无论是在哪种逻辑判断的题型里,都会运用到翻译推理里面的知识。今天我们就来学习翻译推理中运用最多的推理规则——逆否定理。
什么叫做逆否定理?用简单的口诀来记忆,可以称之为“肯前必肯后,否后必否前,否前肯后无必然”。这里的前后分别指的是什么呢?是翻译表达式中的位置指代。假如有翻译表达式“A→B”,那么推出箭头“→”的左边我们称之为前件,推出箭头的右边我们称之为后件,逆否定理中的前后也与之对应。若题目中出现了“否前也否后”这样的选项,根据逆否定理,我们便可以进行排除,由此得到正确答案。
那在题目中如何进行运用呢?我们来做几道例题感受一下。
【例1】刑警王某从某个杀人现场勘查完毕回到局里。门卫老张问他结果怎么样,王某说知道了杀人犯到过现场。老张知道王某在调侃他,因为根本无须王某告诉,他就知道:如果某人是杀人犯,那么案发时他一定在现场。
但据此回答,我们可以推知:
A.如果张三案发时在现场,那么他就是杀人犯
B.如果李四不是杀人犯,那么案发时他就不在现场
C.如果王五案发时不在现场,那么他就不是杀人犯
D.即使许六不在案发现场,也有可能是杀人犯
【答案】C
【解析】第一步,确定题型。
根据题干关联词“如果……那么……”,确定为翻译推理。
第二步,翻译题干。
①杀人犯→在现场
第三步,进行推理。
A项:“在现场”是对①的“肯后”,肯后推不出必然结论,排除;
B项:“不是杀人犯”是对①的“否前”,否前推不出必然结论,排除;
C项:“不在现场”是对①的“否后”,根据“否后必否前”可得到:“不是杀人犯”,可以推出;
D项:“不在现场”是对①的“否后”,根据“否后必否前”可得到:“不是杀人犯”,排除。
因此,选择C选项。
通过上题大家可以看出,逆否定理在翻译推理中的运用是非常广泛的。
【例2】在知识经济时代,社会持续发展的前提之一是培养大量高素质人才,只有高校教育质量的提升才能培养出大量高素质人才,而高校教育质量的提升一定要求高校教师整体素养的提升。
如果以上陈述为真,则可以推出以下哪项?
A.只要社会持续发展,就要求提升高校教师整体素养
B.如果没有大量高素质人才,那么高校教育质量不会有提升
C.如果培养了大量高素质人才,那么社会就能持续发展
D.如果处在知识经济时代,高校教育质量必定有所提升
【答案】A
【解析】第一步,确定题型。
根据题干逻辑关联词“只有……才……”,确定为翻译推理。
第二步,翻译题干。
①社会持续发展→培养大量高素质人才
②培养大量高素质人才→高校教育质量提升
③高校教育质量提升→高校教师整体素养提升
以上条件可以递推出:④社会持续发展→高校教师整体素养提升
第二步,辨析选项。
A项:翻译为:社会持续发展→提升高校教师整体素养,是对④的肯前,肯前必肯后,可以推出,正确;
B项:翻译为:没有大量高素质人才→高校教育质量不会提升,是对②的否前,否前得不出必然结论,无法推出,排除;
C项:翻译为:培养大量高素质人才→社会持续发展,是对①的肯后,肯后得不出必然结论,无法推出,排除;
D项:翻译为:知识经济时代→高校教育质量提升,题干中“知识经济时代”和“高校教育质量提升”之间没有推出关系,无法推出,排除。
因此,选择A选项。
数量关系备考技巧:工程问题巧赋值
说到公考,不少考公人的瞬间反应便是:要考很多模块,需要上知天文下知地理,尤其是数量关系简直难于登天!
那么,作为一名经验丰富的数资老师,客观来说,数量关系这个模块确实会出难题,比如:排列组合问题、行程问题、几何问题等,但并不是所有题都难,比如:工程问题,只要我们掌握了方法,轻轻松松让你对的稀里糊涂,不信我们一起来看。
那么,我们一般把有什么特征的题型界定为工程问题呢?其实,现实生活中比较常见的涉及到工程量的问题,都可以理解为狭义上的工程问题,比如:修桥、铺路,建学校等等。但从广义上来说,只要涉及完成一件事情需要多长时间的问题,都可以理解为工程问题。
那么,在工程问题中,我们需要掌握一些什么知识点才能解决这类问题呢?
接下来我们一起认识一下工程问题的知识点和解题思路。
1、核心公式:
工作总量=工作效率×工作时间
注:(1)当工作效率一定的情况下,工作总量与工作时间呈正比例;
(2)当工作时间一定的情况下,工作总量与工作效率呈正比例;
(3)当工作总量一定的情况下,工作时间与工作效率呈反比例。
2、高频考法题干特征
给定时间型:题目中只给定不同主体的完工时间,其余量未知;
效率制约型:题目中不仅给定工作时间,还给出效率的比例倍数关系。
3、解题思路:赋值法
给定时间型:先赋工作总量为时间的公倍数,再求效率,最后求所求量;
效率制约型:先按照效率比赋值效率,再求工作总量,最后求所求量。
看吧,是不是非常好理解。那接下来我们一起来看看这两种高频考法在真题中具体是以什么样子呈现的?又是如何用方法来解题的?
【例1】一项工程由甲、乙工程队单独完成,分别需50天和80天。若甲、乙工程队合作20天后,剩余工程量由乙、丙工程队合作需12天完成,则丙工程队单独完成此项工程所需的时间是:
A. 40天
B. 45天
C. 50天
D. 60天
【答案】D
【解析】第一步,本题考查工程问题,属于给定时间型,用赋值法解题。

因此,选择D选项。
【例2】甲工程队与乙工程队的效率之比为4:5,一项工程由甲工程队单独做6天,再由乙工程队单独做8天,最后由甲、乙两个工程队合作4天刚好完成,如果这项工程由甲工程队或乙工程队单独完成,则甲工程队所需天数比乙工程队所需天数多多少天?
A. 3
B. 4
C. 5
D. 6
【答案】C

至此,相信大家对工程问题有了一个基本的了解和掌握,所以说想要顺利高分上岸,其实并不是完全放弃数量关系,而是选择出不难的部分快速拿分。正所谓:良禽择木而栖,我们公考测试的是大家合理取舍的能力,而对于数量关系,我们就把像工程问题这一类简单且高频的考点稳稳拿下,那么上岸便指日可待了。
最后,再给大家巩固和总结一下这部分的知识点。

图形备考——对称常见考点
在行测考试中,对称图形是图形推理经常考到的图形,而且它的考点变化大,出题形式多样化,给考试增加了难度。因此,本文就带着大家来了解一下关于对称图形的结构考查方式。
一、对称图形的分类
在图形推理的题目中,常见的对称图形主要分为三种类型:轴对称图形、中心对称图形和轴+中心对称图形。
轴对称图形:如果一个图形沿着一条直线对折后两部分完全重合,那么这个图形叫做轴对称图形。如字母图形“B”,或等腰三角形等。轴对称图形的对称轴条数可以为1条或者多条;对称轴的方向可分为横轴、纵轴、斜轴等。
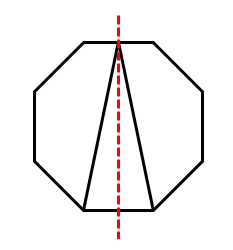
中心对称图形:如果一个图形绕某一点旋转180度,旋转后的图形能和原图形完全重合,那么这个图形叫做中心对称图形。如字母图形“z”,或者平行四边形等。
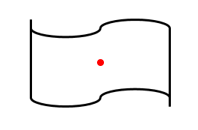
轴+中心对称图形:如果图形既是轴对称图形、又是中心对称图形,那么这个图形叫做轴+中心对称图形。如字母图形“H”,或者正多边形(如四角星、六边形)等。值得注意的是一个图形既轴对称又中心对称一定有两条或两条以上的对称轴。
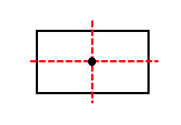
除此之外,各位考生还要注意旋转对称图形。旋转对称图形是指图形围绕着某个点旋转一定的角度(旋转角度大于0°,小于360°)后与原图成对称关系的图形。比如五角星就是旋转72°之后可以与原图重合。常见的旋转图形有正多边形,圆,平行四边形等。一般而言,所有的中心对称图形都是旋转对称图形,但是旋转对称图形不一定是中心对称图形。
二、对称图形常见考点
1、对称的类型
当图形形状不一,数量上没有规律或者有明显的对称图形时,可以考虑对称的规律。最常见的就属对称类型的考查了。在这里主要考查的是判别图形是非对称图形还是对称图形,是轴对称图形、中心对称图形还是轴+中心对称图形的能力。
【例1】(2020联考)把下面的六个图形分为两类,使每一类图形都有各自的共同特征或规律,分类正确的一项是:
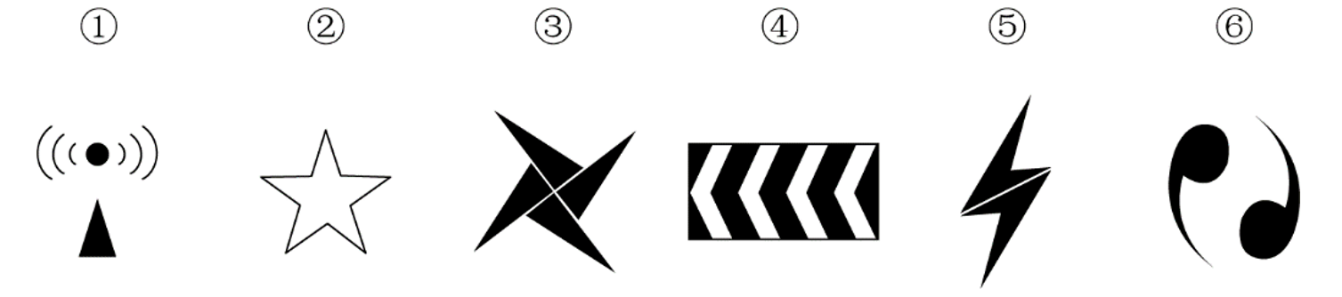
A.①④⑥,②③⑤
B.①③⑥,②④⑤
C.①②⑥,③④⑤
D.①②④,③⑤⑥
【答案】D
【解析】第一步,观察特征。
组成元素不同,优先考虑数量类或属性类,此题对称特征明显,考虑对称性属性。
第二步,根据规律进行分组。
观察发现,图形①②④是轴对称图形,图形③⑤⑥是中心对称图形,分为两组。
因此,选择D选项。
2、对称轴的方向
当出现的图形是轴对称图形,而且图形的对称轴只有一条时,图形的对称轴在方向上往往会呈现出统一或者动态旋转变化一定角度的规律。
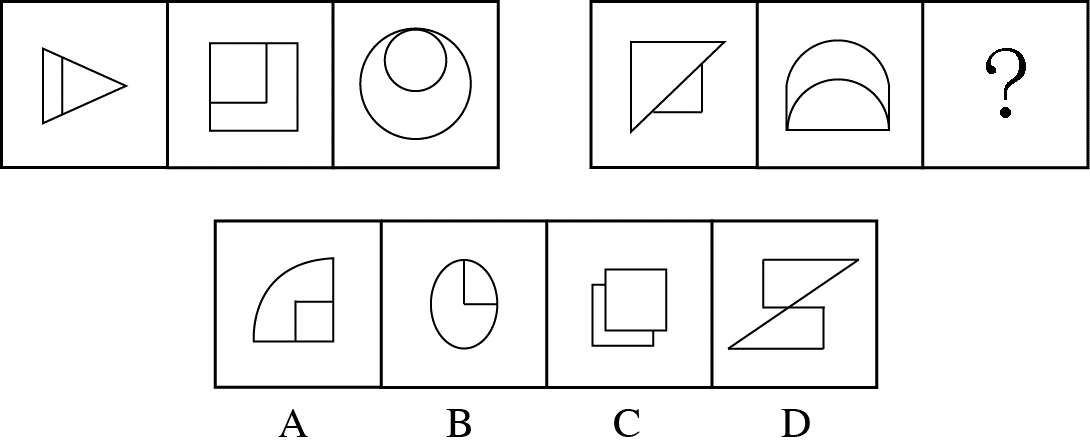
【例2】(2017-国家)从所给四个选项中,选择最合适的一个填入问号处,使之呈现一定规律性:
【答案】C
【解析】第一步,观察特征。
组成元素不同,优先考虑属性类或数量类。对称特征明显,考虑属性类对称性。
第二步,两段式,第一段找规律,第二段应用规律。
第一段三个图形均为轴对称图形,对称轴方向分别为:横轴、斜轴()、竖轴,即对称轴依次顺时针旋转45°;第二段应用规律,前两图的对称轴方向为斜轴()、竖轴,问号处应为斜轴(/),只有C项符合。
因此,选择C选项。
3、对称轴的数量
当出现的图形是轴对称图形,而且图形的对称轴不只一条时,多考查对称轴的数量。图形的对称轴在数量上可能会呈现出常数、等差、运算或者是对称轴的数量与图形中的面、线、角、点的数量之间的关系等规律。
【例3】(2019-山东)从所给的四个选项中,选择最合适的一个填入问号处,使之呈现一定的规律性:

【答案】D
【解析】第一步,观察特征。
组成元素不同,优先考虑数量类或属性类,对称特征明显,考虑属性类对称性。
第二步,九宫格,横向规律较为常见,优先考虑。
第一行中三个图形的对称轴条数分别是1、1、2;第二行中三个图形的对称轴条数分别是1、2、3;前两个图形的对称轴条数之和等于第三个图形的对称轴条数。第三行应用规律,前两个图形的对称轴条数分别为2、3,2+3=5,所以问号处的图形应有5条对称轴,只有D项符合。
因此,选择D选项。
4、对称轴与图形的关系
当出现的轴对称图形在对称轴的数量和方向上找不到规律时,可以观察对称轴与图形中的线是否存在垂直或重合等关系。
【例4】(2020-国家)把下面的六个图形分为两类,使每一类图形都有各自的共同特征或规律,分类正确的一项是:
A.①③④,②⑤⑥
B.①②⑥,③④⑤
C.①④⑤,②③⑥
D.①④⑥,②③⑤
【答案】C
【解析】第一步,观察特征。
图形组成元素不同,优先考虑数量类或属性类,对称特征明显,考虑属性类对称性。
第二步,依据规律进行分组。
图形均有对称性,其中图形①④⑤的对称轴均与原图的线条垂直,图形②③⑥的对称轴均经过原图形的交点,分为两组。
因此,选择C选项。
5、图形与图形之间对称轴的关系
当图形是由若干个对称图形组成的,可以观察各个部分的对称轴之间的关系。
【例5】(2018-国家)从所给的四个选项中,选出最合适的一个填入问号处,使之呈现一定的规律性:
【答案】D
【解析】第一步,观察特征。
组成元素不同,优先考虑数量类或属性类,每幅图形均由两个对称图形组成,考虑对称性。
第二步,两段式,第一段找规律,第二段应用规律。
第一段,每幅图中两个图形对称轴的夹角分别为0°、45°、90°;第二段应用此规律,前两幅图形中两个图形对称轴夹角分别为0°、45°,所以问号处应为90°,如下图所示,只有D项符合。
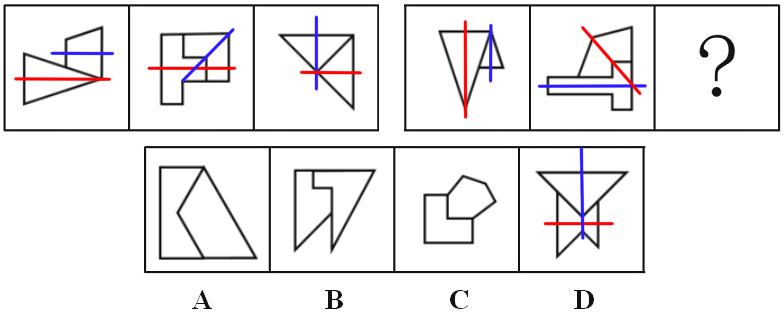
因此,选择D选项。
6、以特殊载体来考查
对称图形通常也会以特殊的载体出现。出题人会利用黑白圆、数字、字母等为载体来考查对称性。我们可以通过观察图形的组成部分及特点来看考查的是什么内容。
①当黑白圆所组成图形中黑色或者白色的部分、有一种情况会考查整体的对称性,而相对特殊的是考查局部的对称性。比如下图考查的就是白色圈圈整体分为轴对称和中心对称。
【例6】(2021-浙江) 把下面的六个图形分为两类,使每一类图形都有各自的共同特征或规律,分类正确的一项是:

【答案】C
【解析】第一步,观察特征。
图形组成不同,考虑数量类或属性类。白色区域较为规整,考虑属性类对称性。
第二步,根据规律进行分组。
图形①②⑥中白球组成的区域为轴对称图形,图形③④⑤中白球组成的区域为中心对称图形,分为两组。
因此,选择C选项。
②另外一种情况,是当类似在一个大白面进行分割,面的特征比较明显。如果数面的个数不构成数量规律的话,我们可以重点看一下最大的白面或最小的白面都具备了什么特征?常见的一种情况是最大的白面会考查是否是轴对称或者是中心对称图形。如图所示主要考查图形中面积最大的部分都是中心对称图形。
【例6】从所给的四个选项中,选出最合适的一个填入问号处,使之呈现一定的规律性:
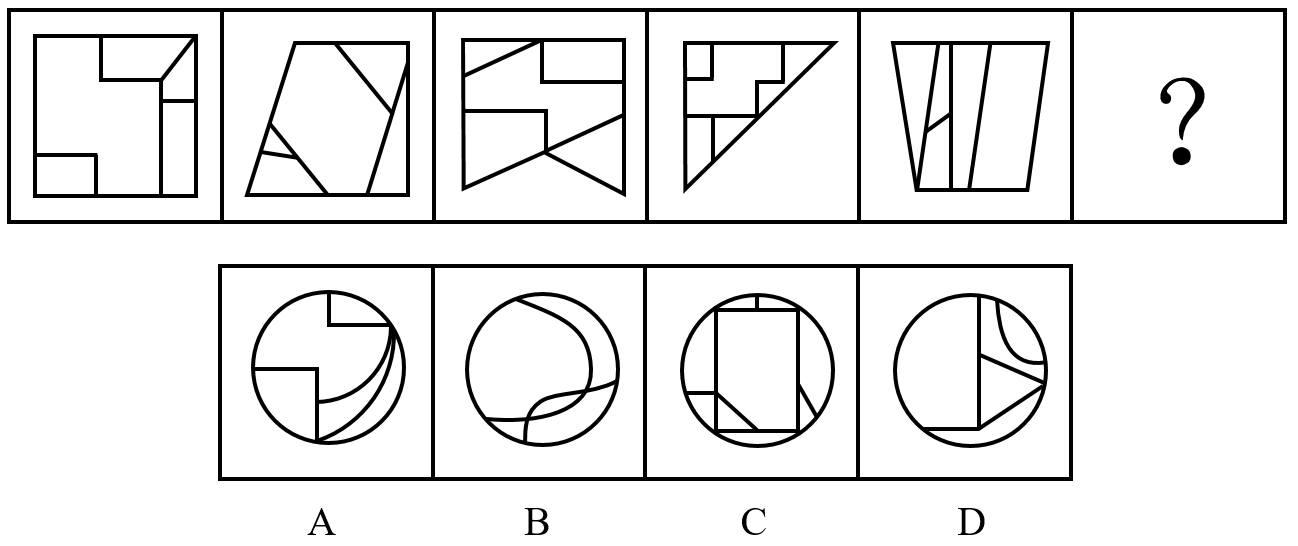
在这个题中我们不难会发现,面很明显,但是答案不唯一。除此之外还要注意到每一个图形都有一个很大的白面。而这个白面刚好全部都是中心对称图形。











